Null models
Contents
Description
In statistics, it is a common task to analyze the statistical significance of a value in which we have interest. Most of the time this task is done by comparing the value in question with a null model. In our case, to analyze the statistical significance of the values of modularity and nestedness giving by a bipartite network we need to compare them with an ensamble of random networks (our null model).
BiMat proposes five null models to test the significance of measured nestedness and modularity. These null models generate random networks through a Bernoulli process, where the probability of interactions are determined following different rules. Define $k_i$ as the degree of a node $i$ of the column class and $d_j$ as the degree of a node $j$ of the row class. Then, the probability that two nodes (of distinct classes) interact, $P_{ij}$ is:
- NullModels.EQUIPROBABLE: $P_{ij} = E/(mn)$ -- the connectance of the network is respected, but not the number of interactions in which each node is involved.
- NullModels.AVERAGE: $P_{ij} = (k_{i}/n + d_{j}/m)/2$ -- the connectance, and the expected number of interactions in which each node is involved, are respected
- NullModels.COLUMNS: $P_{ij} = k_{i}/n$ -- the connectance, and the expected number of interactions of row nodes, are respected
- NullModels.ROWS: $P_{ij} = d_{j}/m$ -- the connectance, and the expected number of interactions of column nodes, are respected
An additional null model that cannot be expressed in terms of cell probabilities and is included in BiMat is:
- NullModels.FIXED: Under this null model the exact sum of rows and columns is respected. A swap algorithm is used in order to get the random matrices.
By default, BiMat generate networks that can have disconnected nodes (i.e. nodes with no edges to any other nodes in the network). However the user can impose a constraint that all nodes must be connected to at least one other node (if possible) in the null model generating process.
Example
The next example shows how to create null model:
%Original matrices that will be used as test nested_matrix = MatrixFunctions.NESTED_MATRIX(20); modular_matrix = MatrixFunctions.BLOCK_MATRIX(2,10); %Setting the seed for reproducibility: rand('seed',100); %Null models from the original nested matrix nested_equiprobable_matrix = NullModels.EQUIPROBABLE(nested_matrix); nested_average_matrix = NullModels.AVERAGE(nested_matrix); nested_row_average_matrix = NullModels.AVERAGE_ROWS(nested_matrix); nested_fixed = NullModels.FIXED(nested_matrix); modular_equiprobable_matrix = NullModels.EQUIPROBABLE(modular_matrix); modular_average_matrix = NullModels.AVERAGE(modular_matrix); modular_row_average_matrix = NullModels.AVERAGE_ROWS(modular_matrix); modular_fixed = NullModels.FIXED(modular_matrix); %Some plot format for all plots plot_format = PlotFormat(); plot_format.use_labels = false; plot_format.back_color = [0.6000,0.7686,1.0000]; plot_format.cell_color = 'white'; font_size = 20; %Plotting figure(1); set(gcf,'position', [22,52,1373,508]); subplot(2,5,1); ylabel('Nested', 'FontSize', font_size); title('Original matrix', 'FontSize', font_size); PlotWebs.PLOT_MATRIX(nested_matrix, plot_format); subplot(2,5,2); title('Equiprobable', 'FontSize', font_size); PlotWebs.PLOT_MATRIX(nested_equiprobable_matrix, plot_format); subplot(2,5,3); title('Average', 'FontSize', font_size); PlotWebs.PLOT_MATRIX(nested_average_matrix, plot_format); subplot(2,5,4); title('Rows Average', 'FontSize', font_size); PlotWebs.PLOT_MATRIX(nested_row_average_matrix, plot_format); subplot(2,5,5); title('Fixed', 'FontSize', font_size); PlotWebs.PLOT_MATRIX(nested_fixed, plot_format); subplot(2,5,6); ylabel('Modular', 'FontSize', font_size); PlotWebs.PLOT_MATRIX(modular_matrix, plot_format); subplot(2,5,7); PlotWebs.PLOT_MATRIX(modular_equiprobable_matrix, plot_format); subplot(2,5,8); PlotWebs.PLOT_MATRIX(modular_average_matrix, plot_format); subplot(2,5,9); PlotWebs.PLOT_MATRIX(modular_row_average_matrix, plot_format); subplot(2,5,10); PlotWebs.PLOT_MATRIX(modular_fixed, plot_format);
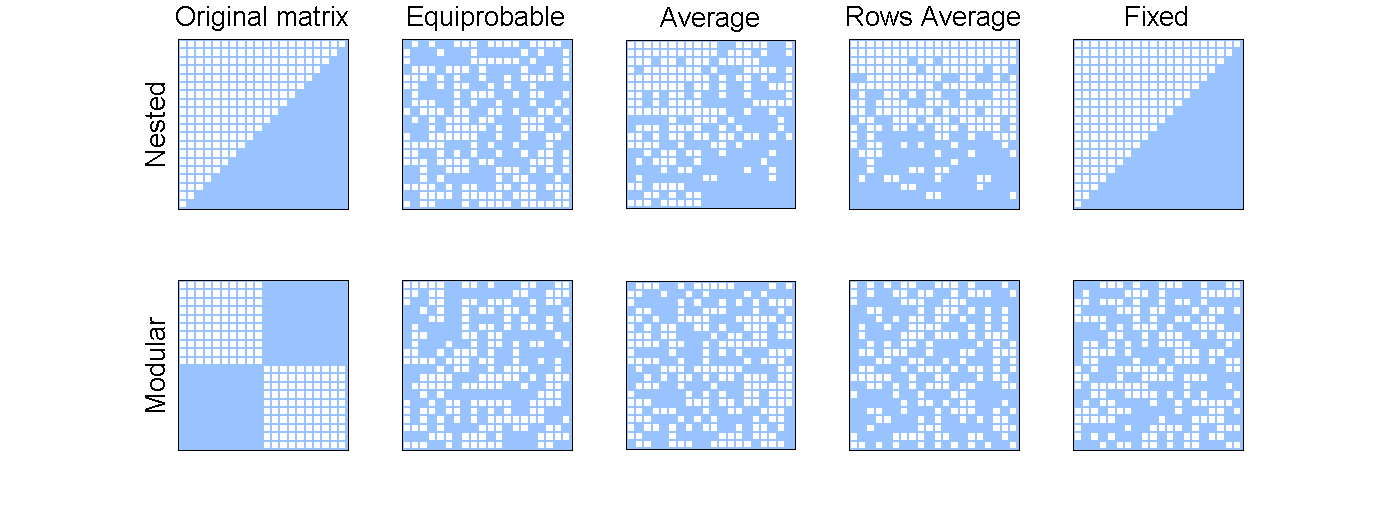
As it is possible to see the chosen null model will have a bigger effect in nested matrices than modular ones.