Network Statistics
As described in the null models section, modularity and nestedness values lack statistical significance if they are not compared with an appropiate null model. Further, an appropiate ensamble of those random networks need to be created in order to analyze those networks. Altought the user can use BiMat null models for designing his own statistical tests, BiMat comes already with an StatisticalTest that helps the user to perform such tests. BiMat comes with statistical test for both modularity and nestedness. These tests can be executed directly on an instance of the Bipartite class (where the property statistics is an instance of the StatisticalTest class, or directly in the adjacency matrix.
Contents
Example: Working directly on a Bipartite instance
This example will show the usual flow to evaluate the significance of modularity and nestedness on an specific matrix. We will use one of the phage bacteria matrices (Zinno 2010) collected on Flores et al 2012.
%loading and creating data load phage_bacteria_matrices.mat; bp = Bipartite(phage_bacteria_matrices.matrices{38}); %Matrices 38 corresponds to Zinno 2010 %A quick visual of how the data looks like: pformat = PlotFormat(); pformat.use_labels = false; pformat.back_color = [110,110,20]/255; pformat.cell_color = 'white'; pformat.use_isocline_module = false; bp.plotter.SetPlotFormat(pformat); font_size = 16; figure(1); set(gcf,'Position', [38,64,1290,435]); subplot(1,3,1); bp.plotter.PlotMatrix; title('Original','FontSize',font_size); subplot(1,3,2); bp.plotter.PlotNestedMatrix; title('Nested','FontSize',font_size);xlabel('Zinno 2010','FontSize',font_size+6); subplot(1,3,3); bp.plotter.PlotModularMatrix; title('Modular','FontSize',font_size);
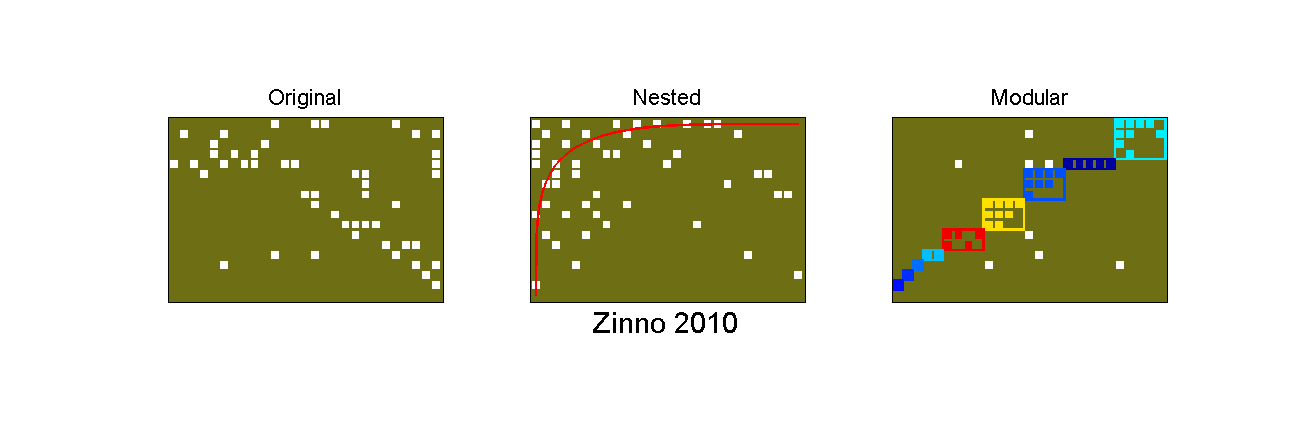
By looking at the last plots, we can infer that this matrix have a strong community structure pattern, while nestedness is not apparent. In order to confirm these observations, we can finally perform nestedness and modularity tests on this matrix (using default values):
bp.statistics.TestCommunityStructure();
Evaluating Modularity in random matrices: 1 - 10 Evaluating Modularity in random matrices: 11 - 20 Evaluating Modularity in random matrices: 21 - 30 Evaluating Modularity in random matrices: 31 - 40 Evaluating Modularity in random matrices: 41 - 50 Evaluating Modularity in random matrices: 51 - 60 Evaluating Modularity in random matrices: 61 - 70 Evaluating Modularity in random matrices: 71 - 80 Evaluating Modularity in random matrices: 81 - 90 Evaluating Modularity in random matrices: 91 - 100
bp.statistics.TestNestedness();
Evaluating Nestedness in random matrices: 1 - 10 Evaluating Nestedness in random matrices: 11 - 20 Evaluating Nestedness in random matrices: 21 - 30 Evaluating Nestedness in random matrices: 31 - 40 Evaluating Nestedness in random matrices: 41 - 50 Evaluating Nestedness in random matrices: 51 - 60 Evaluating Nestedness in random matrices: 61 - 70 Evaluating Nestedness in random matrices: 71 - 80 Evaluating Nestedness in random matrices: 81 - 90 Evaluating Nestedness in random matrices: 91 - 100
As we can see, BiMat shows the status of the current evaluation, which in this case was performed using 100 random matrices (the default value). In order to print the results, the user only need to call the Print method:
bp.statistics.Print;
Modularity Used algorithm: AdaptiveBrim Null model: NullModels.EQUIPROBABLE Replicates: 100 Qb value: 0.6781 mean: 0.5654 std: 0.0257 z-score: 4.3862 t-score: 43.8623 percentil: 100.0000 Qr value: 0.6735 mean: 0.4327 std: 0.0762 z-score: 3.1605 t-score: 31.6053 percentil: 99.0000 Nestedness Used algorithm: NestednessNODF Null model: NullModels.EQUIPROBABLE Replicates: 100 Nestedness value: 0.1247 mean: 0.0941 std: 0.0127 z-score: 2.4022 t-score: 24.0221 percentil: 99.0000
The output just shows the configuration of each evaluation, which in this case was performed using the default values, which may not be a strong statistical test. Let's repeat the experiment using a larger number of random matrices and a different null model:
%The null model will be the AVERAGE one with 1000 replicates: %in the octave version you should replace @NullModels.AVERAGE by 'NullModels.AVERAGE' bp.statistics.DoNulls(1000, @NullModels.AVERAGE); bp.statistics.TestCommunityStructure(); bp.statistics.TestNestedness();
Evaluating Modularity in random matrices: 1 - 100 Evaluating Modularity in random matrices: 101 - 200 Evaluating Modularity in random matrices: 201 - 300 Evaluating Modularity in random matrices: 301 - 400 Evaluating Modularity in random matrices: 401 - 500 Evaluating Modularity in random matrices: 501 - 600 Evaluating Modularity in random matrices: 601 - 700 Evaluating Modularity in random matrices: 701 - 800 Evaluating Modularity in random matrices: 801 - 900 Evaluating Modularity in random matrices: 901 - 1000 Evaluating Nestedness in random matrices: 1 - 100 Evaluating Nestedness in random matrices: 101 - 200 Evaluating Nestedness in random matrices: 201 - 300 Evaluating Nestedness in random matrices: 301 - 400 Evaluating Nestedness in random matrices: 401 - 500 Evaluating Nestedness in random matrices: 501 - 600 Evaluating Nestedness in random matrices: 601 - 700 Evaluating Nestedness in random matrices: 701 - 800 Evaluating Nestedness in random matrices: 801 - 900 Evaluating Nestedness in random matrices: 901 - 1000
And finally printing the results:
bp.statistics.Print();
Modularity Used algorithm: AdaptiveBrim Null model: NullModels.AVERAGE Replicates: 1000 Qb value: 0.6781 mean: 0.5494 std: 0.0487 z-score: 2.6426 t-score: 83.5656 percentil: 99.2000 Qr value: 0.6735 mean: 0.4142 std: 0.1104 z-score: 2.3488 t-score: 74.2749 percentil: 97.8000 Nestedness Used algorithm: NestednessNODF Null model: NullModels.AVERAGE Replicates: 1000 Nestedness value: 0.1247 mean: 0.1072 std: 0.0265 z-score: 0.6583 t-score: 20.8179 percentil: 75.4000
Example: Working using the functional approach
Sometimes the user just want to do a quick analysis, without the extra functionalities that working with a Bipartite instance provides. For those cases, the user can just execute the functional calls of the StatisticalTest class on a specific matrix. Using the previous matrix as an example:
matrix = phage_bacteria_matrices.matrices{38};
%in the octave version you should replace the handle functions by string representations
stest_modul = StatisticalTest.TEST_COMMUNITY_STRUCTURE(matrix,200,@NullModels.AVERAGE,@LeadingEigenvector);
Evaluating Modularity in random matrices: 1 - 20 Evaluating Modularity in random matrices: 21 - 40 Evaluating Modularity in random matrices: 41 - 60 Evaluating Modularity in random matrices: 61 - 80 Evaluating Modularity in random matrices: 81 - 100 Evaluating Modularity in random matrices: 101 - 120 Evaluating Modularity in random matrices: 121 - 140 Evaluating Modularity in random matrices: 141 - 160 Evaluating Modularity in random matrices: 161 - 180 Evaluating Modularity in random matrices: 181 - 200 Modularity Used algorithm: LeadingEigenvector Null model: NullModels.AVERAGE Replicates: 200 Qb value: 0.6822 mean: 0.5529 std: 0.0530 z-score: 2.4424 t-score: 34.5410 percentil: 99.0000 Qr value: 0.7143 mean: 0.4949 std: 0.1069 z-score: 2.0517 t-score: 29.0157 percentil: 97.0000
stest_nest = StatisticalTest.TEST_NESTEDNESS(matrix,200,@NullModels.EQUIPROBABLE,@NestednessNODF);
Evaluating Nestedness in random matrices: 1 - 20 Evaluating Nestedness in random matrices: 21 - 40 Evaluating Nestedness in random matrices: 41 - 60 Evaluating Nestedness in random matrices: 61 - 80 Evaluating Nestedness in random matrices: 81 - 100 Evaluating Nestedness in random matrices: 101 - 120 Evaluating Nestedness in random matrices: 121 - 140 Evaluating Nestedness in random matrices: 141 - 160 Evaluating Nestedness in random matrices: 161 - 180 Evaluating Nestedness in random matrices: 181 - 200 Nestedness Used algorithm: NestednessNODF Null model: NullModels.EQUIPROBABLE Replicates: 200 Nestedness value: 0.1247 mean: 0.0944 std: 0.0137 z-score: 2.2088 t-score: 31.2370 percentil: 98.0000